sample size
2020.10.13 22:13
http://www.quantitativeskills.com/sisa/calculations/samsize.htm
https://sphweb.bumc.bu.edu/otlt/mph-modules/bs/bs704_power/bs704_power_print.html
Sample Sizes for Two Independent Samples, Continuous Outcome
In studies where the plan is to perform a test of hypothesis comparing the means of a continuous outcome variable in two independent populations, the hypotheses of interest are:
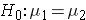
versus
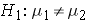
where μ 1 and μ 2 are the means in the two comparison populations. The formula for determining the sample sizes to ensure that the test has a specified power is:
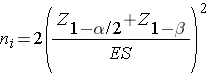
where ni is the sample size required in each group (i=1,2), α is the selected level of significance and Z 1-α /2 is the value from the standard normal distribution holding 1- α /2 below it, and 1- β is the selected power and Z 1-β is the value from the standard normal distribution holding 1- β below it. ES is the effect size, defined as:
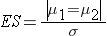
where | μ 1 - μ 2 | is the absolute value of the difference in means between the two groups expected under the alternative hypothesis, H1. σ is the standard deviation of the outcome of interest. Recall from the module on Hypothesis Testing that, when we performed tests of hypothesis comparing the means of two independent groups, we used Sp, the pooled estimate of the common standard deviation, as a measure of variability in the outcome.
Sp is computed as follows:
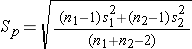
If data are available on variability of the outcome in each comparison group, then Sp can be computed and used to generate the sample sizes. However, it is more often the case that data on the variability of the outcome are available from only one group, usually the untreated (e.g., placebo control) or unexposed group. When planning a clinical trial to investigate a new drug or procedure, data are often available from other trials that may have involved a placebo or an active control group (i.e., a standard medication or treatment given for the condition under study). The standard deviation of the outcome variable measured in patients assigned to the placebo, control or unexposed group can be used to plan a future trial, as illustrated.
Note also that the formula shown above generates sample size estimates for samples of equal size. If a study is planned where different numbers of patients will be assigned or different numbers of patients will comprise the comparison groups, then alternative formulas can be used (see Howell3 for more details).
https://www.statisticshowto.com/what-is-the-continuity-correction-factor/
https://www.researchgate.net/publication/271265621_Sample_size_calculation_on_web_can_we_rely_on_the_results
https://europepmc.org/article/pmc/pmc4751211
댓글 0
| 번호 | 제목 | 글쓴이 | 날짜 | 조회 수 |
|---|---|---|---|---|
| 1701 | CORS | WHRIA | 2021.01.22 | 133 |
| 1700 | popup | WHRIA | 2020.12.31 | 99 |
| 1699 | bay trail ubuntu 20.04 [1] | WHRIA | 2020.12.24 | 57 |
| 1698 | 32 bit UEFI [6] | WHRIA | 2020.12.24 | 205 |
| 1697 | sroc [1] | WHRIA | 2020.12.10 | 61 |
| 1696 | test | WHRIA | 2020.12.03 | 47 |
| 1695 | dkms for r8125 | WHRIA | 2020.11.12 | 96 |
| 1694 | unattended upgrade | WHRIA | 2020.11.01 | 478 |
| 1693 | pytorch pretrained | WHRIA | 2020.10.28 | 150 |
| 1692 | steamlit | WHRIA | 2020.10.15 | 211 |
| » | sample size | WHRIA | 2020.10.13 | 4235 |
| 1690 | Transformer | WHRIA | 2020.10.09 | 155 |
| 1689 | file lock | WHRIA | 2020.09.22 | 99 |
| 1688 | onnx broswer | WHRIA | 2020.09.15 | 42 |
| 1687 | fda 인증 | WHRIA | 2020.09.03 | 213 |